1. Introdução
No último artigo mostramos as funções para cálculo da média, mediana e moda no banco de dados Oracle. O artigo pode ser consultado através do link: //www.devmedia.com.br/calculando-media-moda-e-mediana-no-oracle/25577
Média, mediana e moda são medidas de tendência central, cujo propósito é sintetizar em um único número o que é típico (ou médio) em um conjunto de dados. Porém, estas medidas normalmente irão fornecer apenas um quadro incompleto dos dados. Para exemplificar a o que acabamos de afirmar, considere a tabela CAMPEONATO, mostrada na Figura 1. Esta tabela mostra as infrações cometidas por diversos jogadores que foram expulsos em um campeonato de futebol. As colunas JUIZ_A e JUIZ_B mostram as punições que foram atribuídas por dois juízes do “tribunal de esporte” para cada infração (cada punição é dada em número de jogos).
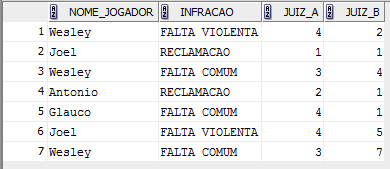
Figura 1: Tabela “Campeonato”
Podemos calcular a média de jogos atribuída nas penas de ambos os juízes com o uso da função AVG, como mostra a Listagem 1. Observe que a média é de 3 jogos tanto para o juiz A como para o juiz B.
Listagem 1: Obtenção da MÉDIA das penas atribuídas pelos Juízes A e B com a função AVG
SELECT AVG(juiz_a), AVG(juiz_b) FROM campeonato
AVG(juiz_a) AVG(juiz_b)
3 3
Será eque podemos concluir que os juízes tem “comportamento igual”, ou seja, que eles utilizam critérios parecidos? Ou será que, de fato, o uso da medida da média isoladamente não foi capaz de apresentar um quadro real da situação?
Para respondermos a essas perguntas, precisaremos fazer uso de outras medidas estatísticas. Precisaremos usar medidas de variabilidade, pois elas são capazes de fornecer um índice da dispersão dos escores em torno da média. As próximas seções apresentam essas medidas e a sua forma de utilização no SGBD Oracle.
2. Amplitude
Amplitude é uma medida rápida da variabilidade. Ela consiste na diferença entre o mais alto e o mais baixo valor de um determinado conjunto de dados (ou seja, de um determinado campo numérico da tabela Oracle). Na linguagem SQL, podemos calcular a amplitude com o uso das funções MAX e MIN, como mostra a Listagem 2.
Listagem 2: Obtenção da AMPLITUDE com as funções MAX e MIN
SELECT
(MAX(juiz_a) - MIN(juiz_a)) as Amplitude_A,
(MAX(juiz_b) - MIN(juiz_b)) as Amplitude_B
FROM campeonato
Amplitude_A Amplitude_B
3 6
A amplitude do Juiz A é igual a 3, pois a sua maior pena foi de 4 jogos e a menor de 1 jogo (4 – 1 = 3). Já a amplitude do Juiz B é igual a 6, pois a sua maior pena foi de 7 jogos e a menor de 1 jogo (7 – 1 = 6). Com isto, já podemos perceber que a distribuição das penas do Juiz B apresenta uma maior variabilidade do que a do Juiz A.
No entanto, na prática a amplitude não é uma medida muito boa. Ela tem a vantagem de ser simples e rápida de calcular. Porém tem a desvantagem de depender apenas de dois valores de toda a distribuição (o menor valor e o maior valor). Com isso, ela pode ser claramente influenciada por um único valor. Precisamos então de medidas que levem em conta todos os valores da distribuição. Essas medidas são a Variância e o Desvio Padrão.
3. Variância e Desvio Padrão
Para entendermos a variância, inicialmente precisamos apresentar o conceito de desvio que consiste na distância de um valor arbitrário ao valor médio da variável. O desvio é normalmente representado com a notação mostrada na Figura 2.
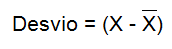
Figura 2: Fórmula do Desvio
Nesta fórmula, o X que contém o traço em cima representa o valor da média da variável. O X sem o traço é um valor qualquer. Retornando aos dados da Figura 1, podemos os desvios para cada escore das variáveis Juiz_A e Juiz_B (pena atribuída pelos juízes A e B) podem ser calculados da forma mostrada a seguir:
Juiz_A
- Desvio Pena 1: (4-3) = 1
- Desvio Pena 2: (1-3) = -2
- Desvio Pena 3: (3-3) = 0
- Desvio Pena 4: (2-3) = -1
- Desvio Pena 5: (4-3) = 1
- Desvio Pena 6: (4-3) = 1
- Desvio Pena 7: (3-3) = 0
Juiz_B
- Desvio Pena 1: (2-3) = -1
- Desvio Pena 2: (1-3) = -2
- Desvio Pena 3: (4-3) = 1
- Desvio Pena 4: (1-3) = -2
- Desvio Pena 5: (1-3) = -2
- Desvio Pena 6: (5-3) = 2
- Desvio Pena 7: (7-3) = 4
Observe que a soma dos desvios é sempre igual a zero. Outra coisa que pode ser facilmente observada é que, em geral, os desvios associados aos escores do Juiz B são maiores do que os do Juiz A. A medida da variância utiliza todos esses escores para que possamos obter um valor de variabilidade. A fórmula da variância é mostrada na Figura 3.
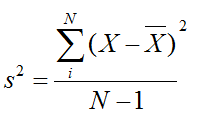
Figura 3: Fórmula da Variância
A fórmula pode parecer um pouco “difícil”, mas não se preocupe, pois você conseguirá entendê-la. Para começar, na equação, s2 é simplesmente o símbolo usado para a variância. O que a medida faz é simplesmente elevar ao quadrado o valor de cada desvio em relação à média e depois somar todos os resultados (numerador da fórmula). Por fim, o valor da soma é dividido por N-1, que corresponde ao número total de escores menos 1 (em nosso exemplo, são N = 7, que representa o número total de registros de nossa tabela. Logo N – 1 = 6). A ideia de elevar ao quadrado é usada simplesmente para eliminar os sinais negativos de alguns desvios.
Veja o exemplo do cálculo da variância para as variáveis Juiz_A e Juiz_B.
Cálculo da Variância - Juiz A
- (4-3)^2 = 1^2 = 1
- (1-3)^2 = -2^2 = 4
- (3-3)^2 = 0^2 = 0
- (2-3)^2 = -1^2 = 1
- (4-3)^2 = 1^2 = 1
- (4-3)^2 = 1^2 = 1
- (3-3)^2 = 0^2 = 0
- SOMA = 8
VAR(Juiz_A) = 8 / 6 = 1,333
Cálculo da Variância - Juiz B
- (2-3)^2 = -1^2 = 1
- (1-3)^2 = -2^2 = 4
- (4-3)^2 = 1^2 = 1
- (1-3)^2 = -2^2 = 4
- (1-3)^2 = -2^2 = 4
- (5-3)^2 = 2^2 = 4
- (7-3)^2 = 4^2 = 16
- SOMA = 34
VAR(Juiz_B) = 34 / 6 = 5,667
Felizmente, o Oracle já possui uma função pronta para o cálculo da variância, denominada, simplesmente variance. O seu uso via SQL é bem simples, como mostra a Listagem 3.
Listagem 3: Obtenção da VARIÂNCIA com a função VARIANCE
SELECT
VARIANCE(juiz_a),VARIANCE(juiz_b)
FROM campeonato
VARIANCE(juiz_a) VARIANCE(juiz_b)
1,3333333333 5,66666666667
A variância considera todos os valores da distribuição, oferecendo uma vantagem sobre amplitude que considera somente dois valores. Por isso ela é mais sensível ao grau de desvio da distribuição de escores. No entanto, um problema da variância é a sua interpretação difícil. Como no numerador da fórmula, os valores dos desvios são elevados ao quadrado, a unidade original de medida acaba sendo alterada. Por exemplo: de número de jogos, para número de jogos ao quadrado. Ou seja, o valor 1,333 para a variância significa 1,333 jogos ao quadrado.
Para corrigir esse problema, podemos utilizar a medida de desvio padrão. Essa medida consiste na raiz quadrada da variância e é usada simplesmente para colocar o valor da variabilidade na unidade original. A Figura 4 mostra a fórmula do desvio padrão, que é representado pela letra “s” (veja que a fórmula é apenas a raiz da fórmula da variância).
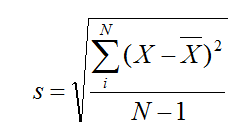
Figura 4: Fórmula do Desvio Padrão
O seja, o desvio padrão da variável Juiz_A é dado por raiz de 1,333 = 1,154. E o desvio padrão da variável Juiz_B é dado por raiz de 5,667 = 2,381. A interpretação que podemos dar para estes valores é a seguinte: em média, as penas atribuídas pelo Juiz_A se afastam da média por apenas 1,154 jogos. Já no caso do Juiz_B, em média, suas penas se afastam da média por mais de 2 jogos (2,381). Isso quer dizer que as penas do Juiz_B apresentam maior variabilidade (talvez ele, por exemplo, seja mais rigoroso para atribuir penas de jogadores reincidentes).
O Oracle também possui uma função pronta para o cálculo do desvio padrão:a função stddev (de “standard deviation”, desvio padrão em inglês). A Listagem 4 apresenta um exemplo de utilização.
Listagem 4: Obtenção do DESVIO PADRÃO com a função STDDEV
SELECT
STDDEV(juiz_a),STDDEV(juiz_b)
FROM campeonato
STDDEV (juiz_a) STDDEV (juiz_b)
1,154700 2,380476
Com isso, encerramos nosso artigo sobre medidas estatísticas para variabilidade no Oracle.