Redes Neurais Artificiais: Algoritmo Backpropagation
Veja neste artigo uma introdução ao algoritmo backpropagation para Redes Neurais Artificiais multi-camadas.
Iremos abordar neste artigo um algoritmo para treinamento de Redes em Multi-Camadas baseado no Aprendizado Supervisionado por Correção e Erro.
Em primeiro lugar vale ressaltar que este assunto se aplica a RNA (Redes Neurais Artificiais) e tem como principal objeto o aprendizado supervisionado de determinada rede dada uma série de padrões. Em outras palavras: você poderá desenvolver um software capaz de aprender, dado os padrões a ele ensinados.
Suponha, por exemplo, que você deseje que seu software calcule os valores do Seno sem programar explicitamente a fórmula do seno, isto é, no seu código não terá uma linha sequer dizendo algo como “return sen(x)”. E como faremos o software retornar o valor do seno se não programarmos isso? Através das RNA, mais especificamente do algoritmo backpropagation.
Como você acha que os radares policiais conseguem captar a placa do seu carro? Como eles conseguem ler letra por letra e dizer que aquela placa é do João? Como eles sabem que aquilo é uma letra A mesmo estando toda borrada e com falhas? Através das RNA.
Este artigo é apenas introdutório e visa explicar de forma mais sucinta possível e de fácil entendimento o funcionamento do backpropagation, porém é altamente recomendável que você tenha uma boa base matemática antes de dar prosseguimento ao mesmo, isso porque você precisará entender os conceitos matemáticos para aplicar o algoritmo na prática.
O Algoritmo Backpropagation
A RNA conta com inúmeros algoritmos para reconhecimento de padrões: Kohonen, Perceptron, Adaline, Backpropagation e muitos outros, cada um com sua especificidade. A principal vantagem em se usar o Backpropagation é que o mesmo trabalha com multicamadas e resolve problemas “não-linearmente separáveis” e alguns algoritmos não resolvem.
Em resumo, um problema “não-linearmente separável” é aquele onde não poderemos separar 2 classes distintas no eixo cartesiano bidimensional apenas traçando uma reta. Na Figura 1 temos um exemplo claro disso.
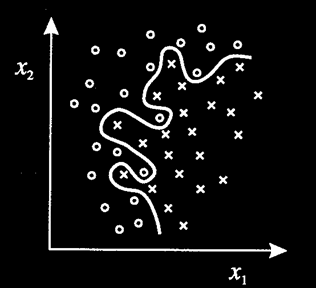
Figura 1: Problema não-linearmente separável
Perceba que não é possível separar o padrão “o” do padrão “x” apenas traçando uma reta. Isso significa que se você tiver como objetivo identificar se aquele objeto é redondo ou quadrado e em algum momento esses padrões apresentam a característica acima, algoritmos que não resolvem problemas desse tipo não serão capazes de distinguir redondo de quadrado.
Outra característica importante é que o Backpropagation é feedforward, ou seja, a conexão entre os neurônios não é cíclica, indo do inicio até o fim você não encontrará um ciclo.
Como funciona
Em qualquer RNA temos os seguintes itens: Neurônios e Pesos. Os neurônios armazenam os valores que serão calculados para definição dos Pesos, onde estes pesos são a “chave” para funcionamento de toda RNA, é pelo peso que a RNA consegue identificar que aquele objeto é redondo e não quadrado.
O Backpropagation é multicamada, pois tem no mínimo 3 camadas. Na Figura 2 você pode ver um Backpropagation de 3 camadas simples apenas para efeito didático.
Figura 2: Algoritmo Backpropagation
Temos então 4 neurônios de entrada (x1, x2, x3 e x4), onde cada um destes se liga a todos os neurônios intermediários (camada oculta ou hidden layer) e cada neurônio da camada oculta se liga a todos os neurônios da camada de saída.
Vamos a um exemplo prático: suponha que você deseje que esta rede aprenda um padrão de loteria (supondo que este sorteio seja “viciado” e que siga um padrão), neste sorteio você pode escolher apenas 2 valores que variam de 0 a 10. Para tentar descobrir este padrão pegaremos 4 variáveis de cada sorteio: data sem caracteres especiais, hora sem caracteres especiais, quantidade de vencedores e valor do prêmio sem decimais.
Suponha então que temos 4 sorteios com a seguinte tabela:
| Data | Hora | Qtd. Vencedores | Prêmio |
|---|---|---|---|
| 10/05/2012 | 10:00 | 13 | 20.000 |
| 10/06/2012 | 10:30 | 20 | 10.000 |
| 11/07/2012 | 09:00 | 21 | 10.500 |
| 11/08/2012 | 09:00 | 10 | 22.000 |
Tabela 1: Lista de Valores para entrada
Transformando essa tabela para nossos neurônios de entrada, ficaria algo como:
- 1 – 10052012, 1000, 13, 20000
- 2 – 10062012, 1030, 20, 10000
- 3 – 11072012, 0900, 21, 10500
- 4 – 11082012, 0900, 10, 22000
Cada uma dessa linha tem 2 saídas desejadas, que são os números sorteados nesta data. Dendo assim, na Figura 2 teremos de treinar nossa rede para aprender essas 4 linhas, assim podemos ver se ela consegue reconhecer um novo padrão que ainda não ocorreu, um novo sorteio que ainda vai ocorrer.
No caso prático acima, nossos x1, x2, x3 e x4 serão respectivamente a Data, Hora, Quantidade de Vencedores e Valor do prêmio. Os nossos Y1 e Y2 serão os números sorteados para cada entrada.
Quando você entra com os valores “x1 = 10052012, x2 = 1000, x3 = 13, x4 = 20000” você deseja que o resultado seja “y1 = 5 e y2 = 10” (resultados deste sorteio). Então quando você submete essa entrada a RNA ela faz os cálculos necessários e retorna y1 = 4.3 e y2 = 4. Significa que ela errou um pouco no y1, mas erro muito no y2, o que fazer? Passar mais um padrão (sorteio 2) e esperar que ela consiga acertar com mais precisão, e se errar muito novamente? Passe outro padrão até ficar o mais próximo possível do resultado desejado.
Toda vez que você submete um padrão e um determinado resultado desejado para este padrão, ela regula os pesos (que são as linhas que conectam os neurônios) para tentar chegar o mais próximo possível do resultado que você deseja, assim quando você submeter um padrão que você não sabe o resultado desejado (que é o caso de um novo sorteio), ela deverá responder o mais próximo possível do resultado real, pois conseguiu aprender esse padrão.
Se você desejar conhecer mais sobre RNA e o algoritmo backpropagation, na seção de links você encontrará materiais de estudo.
Conclusão
É claro que esta foi uma visão bem abstrata do funcionamento real do Algoritmo Backpropagation. Dentro dos cálculos realizados pelos neurônios da camada oculta e de saída há muitos cálculos envolvidos no processo para se reajustar o peso de forma adequada. Na Figura 3 você pode ver um exemplo mais detalhado isso.
Figura 3: Funcionamento do Backpropagation com maior nível de detalhe
Artigos relacionados
-
DevCast
-
DevCast
-
DevCast
-
DevCast
-
DevCast
