Problemas são questões propostas em busca de uma solução. Com o propósito de conceder uma solução para certo problema, existem os algoritmos, cada problema que é decidível possui um algoritmo que determina uma solução para cada instância desse problema.
Algoritmos descrevem passo a passo os procedimentos para chegar a uma solução de um problema e podem ser representados de três formas:
- A forma de descrição narrativa, na qual se usa a linguagem nativa de quem escreve. Essa forma não segue um padrão definido e pode sofrer várias interpretações por quem lê;
- Outra forma de representar um algoritmo é o fluxograma, uma representação visual que utiliza símbolos que são figuras geométricas, cada uma com sua função específica. Essa representação, como o próprio nome diz, mostra o fluxo do algoritmo e também elimina as várias interpretações que a descrição narrativa permitia sobre um algoritmo;
- Por último, existe a linguagem algoritma (Pseudocódigo ou Portugol) que é a que mais se aproxima da estrutura de uma linguagem estruturada.
Um tipo de algoritmo muito usado na resolução de problemas computacionais são os algoritmos de ordenação, que servem para ordenar/organizar uma lista de números ou palavras de acordo com a sua necessidade. As linguagens de programação já possuem métodos de ordenação, mas é bom saber como funcionam os algoritmos, pois há casos de problemas em que o algoritmo de ordenação genérico não resolve, às vezes é necessário modificá-lo.
Os mais populares algoritmos de ordenação são: Insertion sort, Selection sort, Bubble sort, Comb sort, Quick sort, Merge sort, Heap sort e Shell sort. Neste artigo serão estudados os algoritmos Bubble sort, Selection Sort, Quick sort e o Insertion sort, explicando o funcionamento de cada um deles.
Definição de Algoritmos
O Algoritmo é um esquema de resolução de um problema. Pode ser implementado com qualquer sequência de valores ou objetos que tenham uma lógica infinita (por exemplo, a língua portuguesa, a linguagem Pascal, a linguagem C, uma sequência numérica, um conjunto de objetos tais como lápis e borracha), ou seja, qualquer coisa que possa fornecer uma sequência lógica.
Podemos ilustrar um algoritmo pelo exemplo de uma receita culinária, embora muitos algoritmos sejam mais complexos. Um Algoritmo mostra passo a passo os procedimentos necessários para resolução de um problema.
Descrição Narrativa
A descrição narrativa é o uso da sua língua nativa para descrição dos passos para se resolver um problema.
A vantagem dessa forma de representação é que qualquer um pode fazê-la sem ter conhecimentos avançados.
A desvantagem é que não há um padrão, cada pessoa pode escrever como quiser. Outra desvantagem é a imprecisão, ou seja, a descrição pode não ficar clara e pode-se tirar várias interpretações diferentes de um mesmo algoritmo.
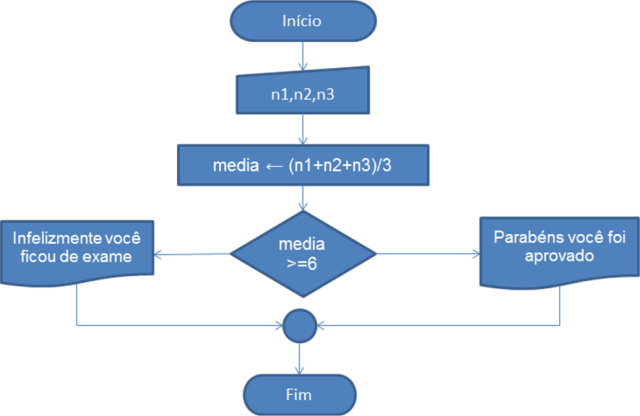
Abaixo temos um exemplo de algoritmo usando a descrição narrativa:
Início
Passo 1: Obter os valores de n1,n2,n3;
Passo 2: Somar os valores do passo 1;
Passo 3: Dividir o resultado obtido no Passo 2 por 3;
Passo 4: Se o resultado do Passo 3 for maior ou igual a 6 então escreva
“Parabéns você foi aprovado”, senão, escreva “Infelizmente você ficou de exame”
e vá para o fim do programa
FimFluxograma
O fluxograma passou a ser usado para eliminar ambiguidades dos algoritmos. São símbolos gráficos padronizados, cada um representado por uma forma geométrica que implica em uma ação, instrução ou um comando distinto.
Esta forma é intermediária a descrição narrativa e ao pseudocódigo, pois é mais precisa do que a primeira, porém, não se preocupa com detalhes de implementação do programa, como os tipos das variáveis usadas.
Linguagem Algoritma (Pseudocódigo ou Portugol)
Essa forma de representação surgiu para tentar suprir as deficiências das outras representações. Consiste na definição de uma pseudolinguagem de programação, cujos comandos são em português, mas que já lembram um pouco a estrutura de uma linguagem de programação estruturada, ou seja, a pseudolinguagem se assemelha muito ao modo como os programas são escritos. Isso vai permitir que os algoritmos sejam traduzidos, quase que diretamente, para uma linguagem de programação.
algoritmo “CalcularMedia”
var
n1,n2,n3,media :real;
inicio
leia(n1,n2,n3);
media← (n1+n2+n3)/3;
se media>=6 entao
escreva(“Parabéns você foi aprovado”);
senão
escreva(“Infelizmente você ficou de exame”);
Fimse
fimalgoritmoAlgoritmos de Ordenação
Algoritmo de ordenação, em ciência da computação, é um algoritmo que coloca os elementos de uma dada sequência em uma certa ordem. Em outras palavras efetua sua ordenação completa ou parcial. O objetivo da ordenação é facilitar a recuperação dos dados de uma lista.
Para este artigo foram escolhidos alguns algoritmos de ordenação para serem estudados que são: Bubble Sort, Selection Sort, Quick Sort e Insertion Sort.
Bubble Sort
Bubble sort é o algoritmo mais simples, mas o menos eficientes. Neste algoritmo cada elemento da posição i será comparado com o elemento da posição i + 1, ou seja, um elemento da posição 2 será comparado com o elemento da posição 3. Caso o elemento da posição 2 for maior que o da posição 3, eles trocam de lugar e assim sucessivamente. Por causa dessa forma de execução, o vetor terá que ser percorrido quantas vezes que for necessária, tornando o algoritmo ineficiente para listas muito grandes.
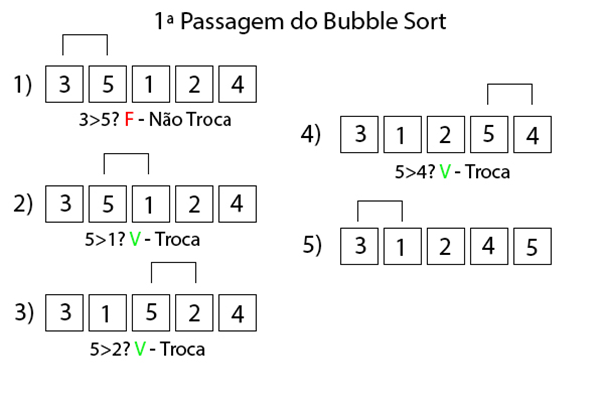
- É verificado se o 3 é maior que 5, por essa condição ser falsa, não há troca.
- É verificado se o 5 é maior que 1, por essa condição ser verdadeira, há uma troca.
- É verificado se o 5 é maior que 2, por essa condição ser verdadeira, há uma troca.
- É verificado se o 5 é maior que 4, por essa condição ser verdadeira, há uma troca.
- O método retorna ao início do vetor realizando os mesmos processos de comparações, isso é feito até que o vetor esteja ordenado.
Selection Sort
Este algoritmo é baseado em se passar sempre o menor valor do vetor para a primeira posição (ou o maior dependendo da ordem requerida), depois o segundo menor valor para a segunda posição e assim sucessivamente, até os últimos dois elementos.
Neste algoritmo de ordenação é escolhido um número a partir do primeiro, este número escolhido é comparado com os números a partir da sua direita, quando encontrado um número menor, o número escolhido ocupa a posição do menor número encontrado. Este número encontrado será o próximo número escolhido, caso não for encontrado nenhum número menor que este escolhido, ele é colocado na posição do primeiro número escolhido, e o próximo número à sua direita vai ser o escolhido para fazer as comparações. É repetido esse processo até que a lista esteja ordenada.
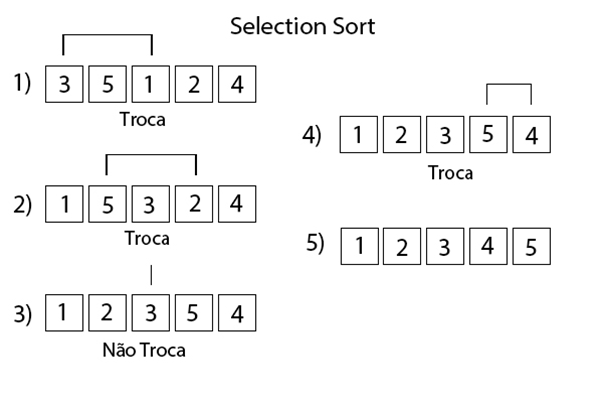
- Neste passo o primeiro número escolhido foi o 3, ele foi comparado com todos os números à sua direita e o menor número encontrado foi o 1, então os dois trocam de lugar.
- O mesmo processo do passo 1 acontece, o número escolhido foi o 5 e o menor número encontrado foi o 2.
- Não foi encontrado nenhum número menor que 3, então ele fica na mesma posição.
- O número 5 foi escolhido novamente e o único número menor que ele à sua direita é o 4, então eles trocam.
- Vetor já ordenado.
Insertion sort
O Insertion sort é um algoritmo simples e eficiente quando aplicado em pequenas listas. Neste algoritmo a lista é percorrida da esquerda para a direita, à medida que avança vai deixando os elementos mais à esquerda ordenados.
O algoritmo funciona da mesma forma que as pessoas usam para ordenar cartas em um jogo de baralho como o pôquer.
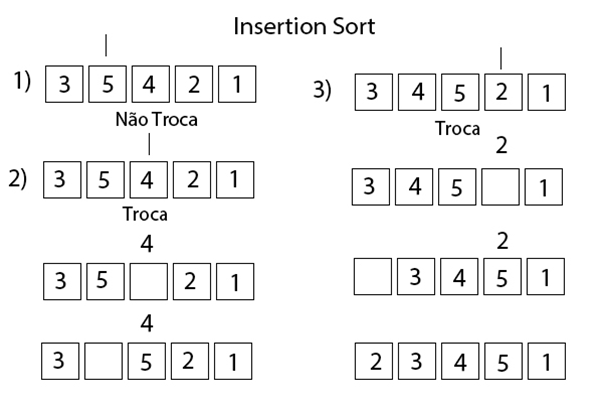
- Neste passo é verificado se o 5 é menor que o 3, como essa condição é falsa, então não há troca.
- É verificado se o quatro é menor que o 5 e o 3, ele só é menor que o 5, então os dois trocam de posição.
- É verificado se o 2 é menor que o 5, 4 e o 3, como ele é menor que 3, então o 5 passa a ocupar a posição do 2, o 4 ocupa a posição do 5 e o 3 ocupa a posição do 4, assim a posição do 3 fica vazia e o 2 passa para essa posição.
O mesmo processo de comparação acontece com o número 1, após esse processo o vetor fica ordenado.
Quick sort
O Quicksort é o algoritmo mais eficiente na ordenação por comparação. Nele se escolhe um elemento chamado de pivô, a partir disto é organizada a lista para que todos os números anteriores a ele sejam menores que ele, e todos os números posteriores a ele sejam maiores que ele. Ao final desse processo o número pivô já está em sua posição final. Os dois grupos desordenados recursivamente sofreram o mesmo processo até que a lista esteja ordenada.
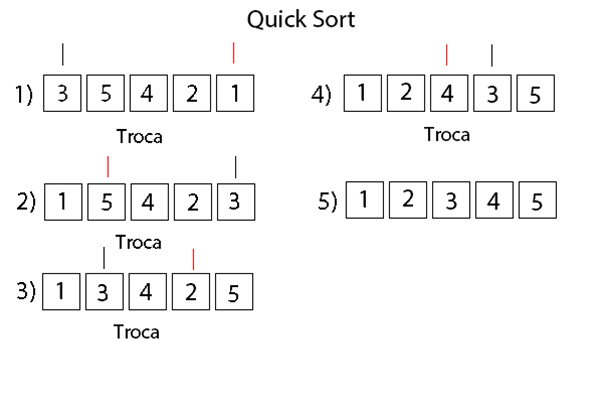
- O número 3 foi escolhido como pivô, nesse passo é procurado à sua direita um número menor que ele para ser passado para a sua esquerda. O primeiro número menor encontrado foi o 1, então eles trocam de lugar.
- Agora é procurado um número à sua esquerda que seja maior que ele, o primeiro número maior encontrado foi o 5, portanto eles trocam de lugar.
- O mesmo processo do passo 1 acontece, o número 2 foi o menor número encontrado, eles trocam de lugar.
- O mesmo processo do passo 2 acontece, o número 4 é o maior número encontrado, eles trocam de lugar.
- O vetor desse exemplo é um vetor pequeno, portanto ele já foi ordenado, mas se fosse um vetor grande, ele seria dividido e recursivamente aconteceria o mesmo processo de escolha de um pivô e comparações.
Estudo de caso
Para realização prática deste artigo, foram feito testes com os algoritmos estudados, os testes foram os seguintes:
Verificar o comportamento dos algoritmos em relação ao tempo, movimentações de trocas e comparações.
Foram testadas 3 ordens de listas com 3 tamanhos diferentes cada:
- Ordem 1: lista ordenada em ordem crescente.
- Ordem 2: lista ordenada em ordem decrescente.
- Ordem 3: lista desordenada com números aleatórios.
Os resultados foram o seguintes:
Ordem 1
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 0,0988 | 5050 | 0 |
| Selection Sort | 0,0602 | 4950 | 297 |
| Insertion sort | 0,0038 | 99 | 198 |
| Quick sort | 0,0141 | 606 | 189 |
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 9,5415 | 500500 | 0 |
| Selection Sort | 5,4587 | 499500 | 2997 |
| Insertion sort | 0,0359 | 999 | 1998 |
| Quick sort | 0,1602 | 9009 | 1533 |
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 934,5364 | 50005000 | 0 |
| Selection Sort | 508,5891 | 49995000 | 29997 |
| Insertion sort | 0,3558 | 9999 | 19998 |
| Quick sort | 2,0824 | 125439 | 17712 |
Ordem 2
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 0,2045 | 5050 | 14850 |
| Selection Sort | 0,0750 | 4950 | 297 |
| Insertion sort | 0,1173 | 99 | 5148 |
| Quick sort | 0,0147 | 610 | 336 |
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 20,3377 | 500500 | 1498500 |
| Selection Sort | 6,9038 | 499500 | 2997 |
| Insertion sort | 11,4277 | 999 | 501498 |
| Quick sort | 0,1622 | 9016 | 3030 |
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 1838,0272 | 50005000 | 149985000 |
| Selection Sort | 665,2050 | 49995000 | 29997 |
| Insertion sort | 1074,1171 | 9999 | 50014998 |
| Quick sort | 2,1279 | 125452 | 32712 |
Ordem 3
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 0,1596 | 5050 | 6777 |
| Selection Sort | 0,0698 | 4950 | 297 |
| Insertion sort | 0,0570 | 99 | 2457 |
| Quick sort | 0,0314 | 897 | 576 |
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 16,6730 | 500500 | 756840 |
| Selection Sort | 5,6664 | 499500 | 2997 |
| Insertion sort | 5,7523 | 999 | 254278 |
| Quick sort | 0,3725 | 13138 | 7983 |
| Algoritmo | Tempo(ms) | Comparações | Movimentações |
|---|---|---|---|
| Bubble sort | 1455,9734 | 50005000 | 74237889 |
| Selection Sort | 545,1068 | 49995000 | 29997 |
| Insertion sort | 539,6891 | 9999 | 24765961 |
| Quick sort | 4,5072 | 176065 | 103635 |
Conclusão
Com base nos testes realizados foram obtidas as seguintes conclusões:
Bubble sort
Para listas já ordenadas em ordem crescente é o único algoritmo que não realiza movimentações, mas em compensação é o que tem o maior tempo e o maior número de comparações. Não só em listas já ordenadas, mas em todos os casos o bubble sort se mostrou um algoritmo ineficiente.
Selection sort
Nas listas de ordem 1 e ordem 3, o selection sort foi o segundo pior algoritmo, mas se mostrou mais eficiente do que o Insertion sort em relação ao tempo e a quantidade de movimentações na lista de ordem 2.
Insertion Sort
Na lista de ordem 1, o Insertion sort se mostrou mais eficiente que todos os outros algoritmos em relação ao tempo e comparações. Na lista de ordem 2 foi menos eficiente do que o selection sort e na lista de ordem 3 a diferença de tempo entre o insertion e o selection foi pequena.
Quick Sort
O quick sort certamente é o algoritmo mais eficiente em listas totalmente desordenadas, ele se torna muito eficiente em relação aos outros no quesito de tempo. Na lista de ordem 3 e na de ordem 2 a diferença de tempo do quick sort em comparação aos outros foi absurdamente grande.