Segurança na Internet hoje em dia é algo bem complexo, pois as pessoas sempre tentam achar uma vulnerabilidade no sistema para poderem se apoderar de informações confidenciais.
Uma pergunta que todo desenvolvedor iniciante sempre se faz, ou pelo menos deveria, é: O que devo fazer para que meu código seja seguro ao ponto de ser 100% inviolável? A resposta dessa pergunta é bem simples: É impossível!
Tudo evolui muito rapidamente no meio da informática, até mesmo as técnicas de invasão, que vem sendo cada vez mais complexas e difíceis de detectar. Mas nada impede ao usuário de criar um código onde ele dará um trabalho maior para quem deseja quebrar sua segurança.
Nesse artigo será abordada uma técnica muita utilizada por bancos para garantir que o usuário que esteja fazendo o login no sistema seja realmente o dono daquelas credenciais.
Implementaremos o algoritmo Time-based One Time Password (TOTP), definido pela RFC6238, o qual utiliza um algoritmo de Hash (HMAC discutido mais a frente) e o UNIX EPOCH para gerar uma sequência de números que mudam depois de um tempo determinado e são responsáveis por autenticar o usuário junto ao sistema.
Existe um outro algoritmo o qual a criação do TOTP foi baseada, que é o HOTP, definido pela RFC4226. Sua lógica é bem parecida, mas ele gera o código de verificação por contagens.
O TOTP, ao ser implementado em uma aplicação, deve ser pensado e arquitetado corretamente, pois por ser um sistema de verificação, deverá ter algum tipo de dispositivo disponibilizado ao usuário que gere corretamente o algoritmo implementado para que ele não tenha problemas ao fazer o login no sistema. Existem empresas que utilizam um hardware externo também conhecido como token, como mostra a Figura 1.

Figura 1. Token TOTP RSA
Esses dispositivos eletrônicos possuem uma chave secreta programada em seu hardware, que é disponibilizada ao cliente pelo fabricante do dispositivo. Essa chave é sigilosa, pois se cair em mão erradas pode causar uma falha de segurança muito grande, possibilitando acessos indesejados a ambientes restritos. Esses dispositivos implementam o TOTP, HMAC e o SHAx em seu hardware, possibilitando assim ter sincronia com o algoritmo que será programado no servidor. Eles também contam com um outro sistema que faz a computação do tempo, porque sem ele não é possível a geração dos códigos de verificação. O problema desses dispositivos é que, eventualmente, perdem a sincronia com o servidor, causando falha na autenticação. Algumas técnicas de sincronia são utilizadas para reverter esse problema como, por exemplo, o Drift time.
Atualmente, com essa nova era de Smartphones e Tablets, muitos aplicativos foram criados para gerar saídas de algoritmos TOTP. Bancos como o Itaú já utilizam o chamado iToken, que é o aplicativo que gera os números de verificação em um Smartphone ou tablet. Existem também aplicativos mais genéricos que foram criados para plataforma tanto Android como iPhone. Um bom exemplo é o Google Authenticator, que dá suporte para algoritmos TOTP e HOTP, como mostrado na Figura 2.
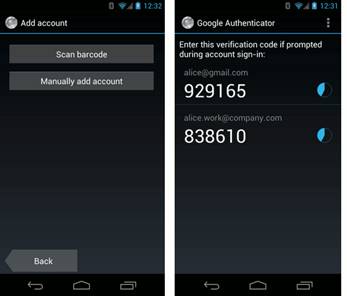
Figura 2. Exemplo de geração de Token via Smartphone
A vantagem de se ter um gerador de token via Smartphone é que ele permite ao usuário inserir manualmente a chave secreta ou fazer um scan via código de barras, o que torna o aplicativo mais genérico e com uma utilização mais ampla pelo usuário. Ao se utilizar um aplicativo genérico de geração de tokens, deve-se ter muito cuidado de não expor a chave secreta, para evitar falhas de segurança.
O fluxo de funcionamento de um TOTP é bem simples (Figura 3), pois ele trabalha com apenas duas variáveis:
- Time: Responsável por ditar de quanto em quanto tempo o código de verificação deve ser alterado;
- Seed: Responsável por gerar a individualidade do código de verificação. Lembre-se que esse código deve-se manter guardado com segurança.
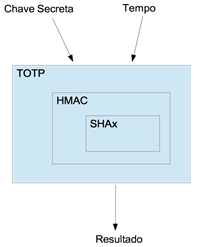
Figura 3. Diagrama simples do TOTP
O tempo no TOTP funciona a partir do UNIX EPOCH (seção Links), que nada mais é que um sistema que define a quantidade de segundos contados desde as 00 horas UTC do dia 1 de janeiro de 1970.
HMAC
O funcionamento do TOTP é possível graças a utilização de um algoritmo chamado HMAC (Hash-based Message Authentication Code) que é definido pela RFC2104, calculando um hash a partir de uma mensagem e uma chave. Esse algoritmo roda obrigatoriamente em cima de um algoritmo de hash (SHA1, SHA256, SHA512), e nesse artigo será usado como base o algoritmo SHA1. Existem muitas bibliotecas que já implementam o HMAC, mas para fins didáticos, ele será explicado e implementado nesse artigo. O próprio Java, dentro do pacote crypto, tem uma implementação do HMAC. Entretanto, como esse pacote abstrai toda a lógica, não é possível visualizar como funciona o cálculo do hash, que é mostrado a seguir:
HMAC(K,M) = SHAx((K XOR opad) | SHAx((K XOR ipad) | M))
Podemos observar o cálculo utilizado para gerar a saída do algoritmo HMAC, onde:
- K: Chave secreta que é a responsável por gerar a individualidade do Hash.
- M: É a mensagem que o Hash será calculado de acordo com o algoritmo e a chave K.
- SHAx: Algoritmo de Hash (Pode ser qualquer versão do SHA).
- opad: Também conhecido como Outer Padding.
- ipad: Também conhecido como Inner Padding.
- XOR: Exclusive OR (Demonstrado mais a frente).
- |: Concatenação.
Na Listagem 1 vemos a implementação desse cálculo.
Listagem 1. Código de implementação HMAC
public class HMAC{
private static final int OPAD = 0x5c;//para RFC2104
private static final int IPAD = 0x36;//para RFC2104
private static final int BLOCKSIZE = 64;//para RFC2104
//Implemenacao RFC 2104
public static byte[] hmac(byte[] key, byte[] message) throws NoSuchAlgorithmException{
byte[] newKey = new byte[64];
byte[] oKeyPad = new byte[64];
byte[] iKeyPad = new byte[64];
byte[] appendedIKey;
byte[] appendedOKey;
byte[] sha1IKey;
int i;
int x = 0;
//Se a chave é maior q o block, tira o hash
if(key.length>BLOCKSIZE)
key = sha1(key);
//Populamos o array newKey com a chave passada e completamos com o byte 0x00
for(i=0;i<BLOCKSIZE;i++){
if(key.length>i)
newKey[i]=key[i];
else
newKey[i]=0x00;
}
//Calculamos o Inner Key Pad e o Outer Key Pad utilizando XOR com duas constantes
for(i=0; i<BLOCKSIZE; i++){
iKeyPad[i] = (byte) (newKey[i]^IPAD);
oKeyPad[i] = (byte) (newKey[i]^OPAD);
}
//Iniciamos o array de Bytes q ira armazenar o append do InnerKey com a menssagem
appendedIKey = new byte[iKeyPad.length+message.length];
//Populamos esse array
for(i=0; i<appendedIKey.length; i++){
if(iKeyPad.length>i){
appendedIKey[i] = iKeyPad[i];
}else{
appendedIKey[i] = message[x];
x++;
}
}
sha1IKey = sha1(appendedIKey);//Executa-se o Hash do InnerKey+Message
x=0;
//Cria-se o array que ira ser populado com a Outer Key + Hash anterior
appendedOKey = new byte[oKeyPad.length+sha1IKey.length];
//Popula esse array
for(i=0; i<appendedOKey.length; i++){
if(iKeyPad.length>i){
appendedOKey[i] = oKeyPad[i];
}else{
appendedOKey[i] = sha1IKey[x];
x++;
}
}
//retorna o resultado.
return sha1(appendedOKey);
}
}É muito importante que o tamanho da chave não exceda o tamanho do blocksize, que é definido como uma das constantes. Se esse tamanho é excedido, um hash é calculado para se adequar ao tamanho.
Quando o hash é calculado, ele pode não ficar do tamanho do blocksize, então o que deve ser feito, é colocar o valor 0x00 nas posições restantes do vetor que guarda a chave secreta.
Listagem 2. Fragmento do Cálculo I
for(i=0; i<BLOCKSIZE; i++){
iKeyPad[i] = (byte) (newKey[i]^IPAD);
oKeyPad[i] = (byte) (newKey[i]^OPAD);
}Na Listagem 2 percebe-se os seguintes fragmentos do cálculo do HMAC: K XOR opad e K XOR ipad.
XOR é o termo curto para eXclusive OR, ou OU Exclusivo. Por exemplo, leve em conta os números 8 e 2. Qual seria o resultado do XOR? 8 ^ 2 = 10. Isso não faz o mínimo sentido se não for levado em consideração que essa operação é binária.
O número 8 em binário é 1000 e o número 2 em binário é 0010: aplicando o XOR o resultado será 1010, que equivale ao número decimal 10. Como o XOR possui uma lógica um pouco diferente, a Tabela 1 demonstra seu funcionamento.
|
A |
B |
A XOR B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Tabela 1. Tabela verdade do XOR
Listagem 3. Fragmento do Cálculo II
appendedIKey = new byte[iKeyPad.length+message.length];
for(i=0; i<appendedIKey.length; i++){
if(iKeyPad.length>i){
appendedIKey[i] = iKeyPad[i];
}else{
appendedIKey[i] = message[x];
x++;
}
}
sha1IKey = sha1(appendedIKey);O código da Listagem 3 demonstra a seguinte parte do cálculo: SHAx((K XOR ipad) | M))
Listagem 4. Fragmento do Cálculo III
x=0;
appendedOKey = new byte[oKeyPad.length+sha1IKey.length];
for(i=0; i<appendedOKey.length; i++){
if(iKeyPad.length>i){
appendedOKey[i] = oKeyPad[i];
}else{
appendedOKey[i] = sha1IKey[x];
x++;
}
}O hash final calculado é representado na Listagem 4, denotando o seguinte fragmento do cálculo: SHAx((K XOR opad) | SHAx((K XOR ipad) | M)).
O resultado retornado é o cálculo completo utilizando o algoritmo HMAC se baseando no algoritmo SHA1. A partir desse ponto pode-se continuar com o TOTP, pois dessa forma que é calculado o hash utilizado para gerar o código a partir do tempo.
TOTP
A implementação do TOTP é, de forma geral, algo bem simples já que a lógica mais complexa se dá ao algoritmo HMAC. Algumas peculiaridades poderão ser notadas, pois o algoritmo utilizará alguns métodos auxiliares para umas conversões de tipos como Hexadecimal para Bytes e String para Hexadecimal. Observe a Listagem 5.
Listagem 5. Algoritmo implementado do TOTP
public class TOTP {
public static String getToken() throws NoSuchAlgorithmException{
String secretSeed = convertStringToHex("12345678901234567890");
String result = null;
long timeWindow = 60L;
long exactTime = System.currentTimeMillis()/1000L;
long preRounded = (long)(exactTime/timeWindow);
String roundedTime = Long.toHexString(preRounded).toUpperCase();
while(roundedTime.length()<16){
roundedTime = "0" + roundedTime;
}
byte[] hash = HMAC.hmac(hexStr2Bytes(secretSeed), hexStr2Bytes(roundedTime));
int offset = hash[hash.length -1] & 0xf;
int otp =
((hash[offset + 0] & 0x7f) << 24) |
((hash[offset + 1] & 0xff) << 16) |
((hash[offset + 2] & 0xff) << 8) |
(hash[offset + 3] & 0xff);
otp = otp % 1000000;
result = Integer.toString(otp);
while(result.length()<6){
result = "0"+result;
}
return result;
}
}Percebam que a secretSeed precisa ser convertida para Hexadecimal, pois se isso não acontecer, o algoritmo não funcionará corretamente. O atributo timeWindow é o responsável por definir o tempo com que o código de segurança será alterado. Aqui foi definido o tempo de mudança em 60 segundos, mas pode ser mudado para outros valores. O tempo é recuperado do EPOCH utilizando a chamada System.currentTimeMillis() e ele é dividido por 1000 para ter um tempo exato em segundos. Logo em seguida, o tempo é arredondado utilizando o número de segundos calculados no exactTime e o mesmo é dividido pelo número de segundos que se deseja ter a mudança do código de verificação. Atentem-se ao preRounded, que não irá se alterar até que o tempo que foi dividido se acabe. Veja nas Figuras 4 a 6 os resultados.

Figura 4. Exact Time vs. Pre Rounded I
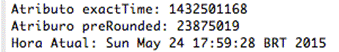
Figura 5. Exact Time vs. Pre Rounded II

Figura 6. Exact Time vs. Pre Rounded III
As Figuras 4 e 5 demonstram claramente que dentro daquele minuto o preRounded não é modificado. Já a Figura 6 mostra essa diferença, o que pode concluir a tese de que o código de verificação será o mesmo até o tempo pré definido se esgote. Após o cálculo do preRounded ter sido concluído, o que se tem a fazer é converter o preRounded do tipo long para uma string hexadecimal. Perceba que tem que ser utilizado o método toUpperCase() para que as letras minúsculas sejam transformadas em maiúsculas.
while(roundedTime.length()<16){
roundedTime = "0" + roundedTime;
}O código apresentado é muito importante para que sejam adicionados zeros a esquerda da String hexadecimal até que se completem 16 posições, como é definido na RCF do TOTP (Listagem 6).
Listagem 6. Núcleo do TOTP
byte[] hash = HMAC.hmac(hexStr2Bytes(secretSeed), hexStr2Bytes(roundedTime));
int offset = hash[hash.length -1] & 0xf;
int otp =
((hash[offset + 0] & 0x7f) << 24) |
((hash[offset + 1] & 0xff) << 16) |
((hash[offset + 2] & 0xff) << 8) |
(hash[offset + 3] & 0xff);
otp = otp % 1000000;
result = Integer.toString(otp);
while(result.length()<6){
result = "0"+result;
}
return result;Primeiramente, em um é necessário que o HMAC seja calculado, passando por parâmetro a Chave Secreta e o Rounded Time já completamente tratado com os zeros adicionados. Também é muito importante reparar que ambos devem ser convertidos de hexadecimal para bytes. O offset, que é um atributo int, recebe o valor da última posição do vetor de bytes hash que acabou de ser calculado pelo HMAC. O operador & é utilizado para fazer a comparação bit a bit entre hash[hash.length -1] e 0xf e armazenar o resultado na variável inteira offset. Segue um exemplo de como funciona o operador &:
int x = 10 & 9;Ao converter 10 e 9 para binário temos 1010 e 1001, respectivamente. Então o resultado será 1000, que é igual a 8 em decimal.
A mágica do algoritmo TOTP ocorre quando se gera o OTP, os números que serão utilizados como resultado final serão extraídos do hash. O operador & será utilizado novamente e em adição a ele será utilizado o operador <<, que é o operador de deslocamento de bits a esquerda utilizando o sinal, como mostra o exemplo a seguir:
x = 2 << 2;Aqui é dito que queremos deslocar a esquerda dois bits do número 2, mas isso não faz nenhum sentido se a base continuar sendo decimal, então convertendo para binário, 2 é 0010. Ao se deslocar dois bits a esquerda o resultado será 1000, que é igual a 8 na base decimal:
0010 << 2 = 1000Listagem 7. Criação do OTP.
int otp =
((hash[offset + 0] & 0x7f) << 24) |
((hash[offset + 1] & 0xff) << 16) |
((hash[offset + 2] & 0xff) << 8) |
(hash[offset + 3] & 0xff);
otp = otp % 1000000;Na Listagem 7, dentro do atributo inteiro otp, é armazenado o resultado dessa lógica e, após isso ocorrer, é calculado o MOD (resto da divisão) e armazenado dentro do atributo otp. Vale ressaltar que o número 1000000 é utilizado para controlar o tamanho do código de verificação que deseja gerar, por exemplo, para um token de seis dígitos, deve-se utilizar otp % 1000000 e para um token de oito dígitos deve-se utilizar otp % 100000000. Também deve-se observar que, ao aumentar o número de zeros no cálculo do MOD no otp, ele deve ser aumentado também no while que o segue, pois o tamanho da string result deve ser equivalente ao número de zeros depois do um, que foi utilizado para calcular o MOD.
Para finalizar o algoritmo é convertido o atributo inteiro opt para String e se o tamanho dela for menor que o tamanho do código de verificação que é desejado, zeros são atrelados a sua esquerda. Pronto, o algoritmo implementado está funcionando corretamente, como pode ser visto na Figura 7.
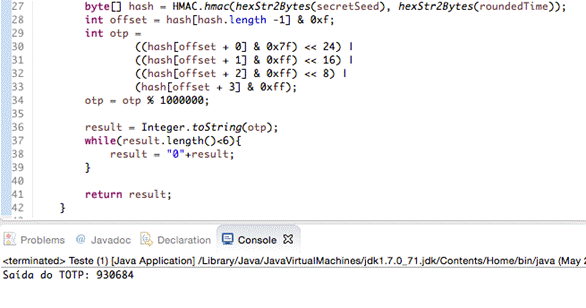
Figura 7. Algoritmo TOTP retornando seu resultado.
Como foi visto, existem alguns métodos auxiliares que foram de extrema ajuda na execução correta do TOTP, que são: hexStr2Bytes e convertStringToHex (Listagem 8 e 9, respectivamente). A partir do momento que o algoritmo trabalha com a manipulação de bytes e informações em hexadecimal, ambos são de suma importância.
Listagem 8. Método auxiliar hexStr2Bytes.
private static byte[] hexStr2Bytes(String hex){
byte[] bArray = new BigInteger("10" + hex,16).toByteArray();
byte[] ret = new byte[bArray.length - 1];
for (int i = 0; i < ret.length; i++)
ret[i] = bArray[i+1];
return ret;
}Listagem 9. Método auxiliar convertStringToHex.
public static String convertStringToHex(String str){
char[] chars = str.toCharArray();
StringBuffer hex = new StringBuffer();
for(int i = 0; i < chars.length; i++){
hex.append(Integer.toHexString((int)chars[i]));
}
return hex.toString();
}Existem várias formas de implementar o TOTP no lado do servidor, normalmente é utilizado em um processo de two-way authentication, ou seja, o usuário abre a página de autenticação e o login e a senha são requisitados pelo servidor. O usuário os digita corretamente e os envia e o servidor os valida em seu banco de dados e, se tudo estiver correto, ele devolve uma mensagem ao usuário requisitando que digite o código de verificação da conta (token). O usuário utilizando seu autenticador genérico favorito ou um fornecido pelo fabricante do software, irá gerar o número de verificação. O servidor receberá a informação enviada e a armazenará em uma variável, e com ela armazenada o servidor buscará em seu banco de dados a chave secreta referente a aquele usuário e executará o algoritmo TOTP utilizando a chave recém recuperada do banco de dados. Assim que tiver o resultado, buscará aquela chave armazenada no início do processo e a comparará com a recém gerada: se as chaves forem iguais, o acesso é liberado e o usuário pode acessar sua área restrita sem problemas, mas se as chaves forem diferentes, o usuário é bloqueado e suas credenciais são requisitadas novamente para uma nova tentativa.
Sincronização
A questão da sincronização com o servidor é algo muito importante que se deve levar em conta. Se acontecer algum problema e um dos dispositivos tiverem o EPOCH dessincronizados por algum evento externo ou alguma falha, o algoritmo não gerará o código de verificação corretamente para o espaço de tempo do servidor. Então, vendo isso e entendendo essa situação, ao se programar uma aplicação que irá utilizar o TOTP é muito importante pensar em uma solução que permita que o aplicativo verifique o servidor e sincronizem seus relógios, para que esse problema não venha a ocorrer e prejudicar a forma com que o sistema é utilizado.
O authenticator do battle.net para celular utiliza essa forma de sincronização de relógios para que o token funcione corretamente, como mostra a Figura 8.

Figura 8. Autenticador battle.net utiliza Sincronização com servidor
Concluindo, a utilização do TOTP em projetos que requerem uma segurança extra é recomendada por gerar uma camada adicional que pode proteger as informações que serão acessadas pelo usuário.
Espero que tenham gostado até a próxima oportunidade.
Links
UNIX EPOCH
http://www.epochconverter.com